First look at Symplectic Topology

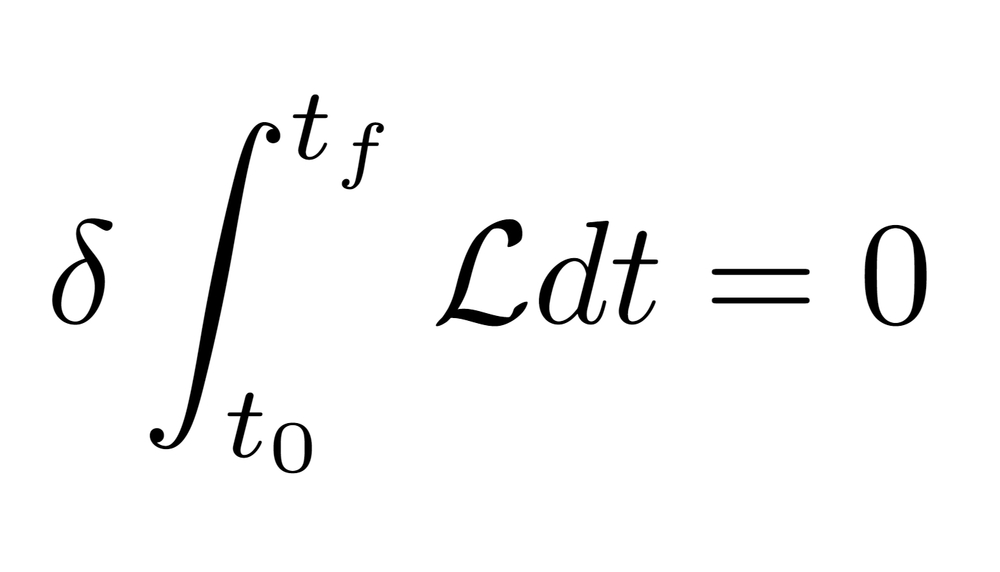
Brief Recap of Lagrangian and Hamiltonian Mechanics

Definition of Lagrangian

Let a $2n+1$-variable function $L(t,x_n,v_n):\mathbb{R}^{2n+1}\rarr\mathbb{R}$ be given, such that:

• it’s twice continously differentiable, so partial derivatives like $\frac{\partial L}{\partial x_i}, \frac{\partial^2 L}{\partial v_i^2}$ are well defined.
• $t$ represent time.
• $x$ is a point in $n$-dimensional Euclidean space, i.e. $x \in \mathbb{R}^n$
• $v_n$ is a derivative at $x$, along any possible curves $\tau$ that passes through $x$, i.e. $v_i=\frac{\partial x}{\partial \tau}$ for any curve $\tau$. We say $v_n$ is in the tangent bundle $T_x\mathbb{R}^n$ of $\mathbb{R}^n$.

This function is called the Lagrangian.

Recall that since Newton’s 2nd law is a second order differential equation, all point particle systems can be specified by their position in space Rn and velocity in tangent bundle TxRn. And since most classical systems can be modelled by Newtonian particles:

• Any rigid bodies are uncountablely infinite number of particles constrainted to have a fixed distance with each other.
• Strings are just an uncountablely infinite number of particles on a 1D line.
• Fluid are just an uncountablely infinite number of particles in a 3D fluid domain.

most classical systems are also only specified by points in some space and their tangent bundles. Evidentially, Lagranians are defined sucht that they takes classical systems as an input and outputs a number.

To model systems using Lagranian mechanics, we choose Lagrangian such that the number it outputs, under the principle of stationary action, give us the equation of motion we want / follows experimental results.

The Principle of Stationary Action

Example:

Lemma 1.1.1 A minimal path

LaTex test: inline Latex:

inline Latex 2: $E=mc^2$

Block latex

Block latex 2:

$$E=mc^2$$

Sources

McDuff, Dusa, and Dietmar Salamon, Introduction to Symplectic Topology, 3rd edn